過去・現在・未来

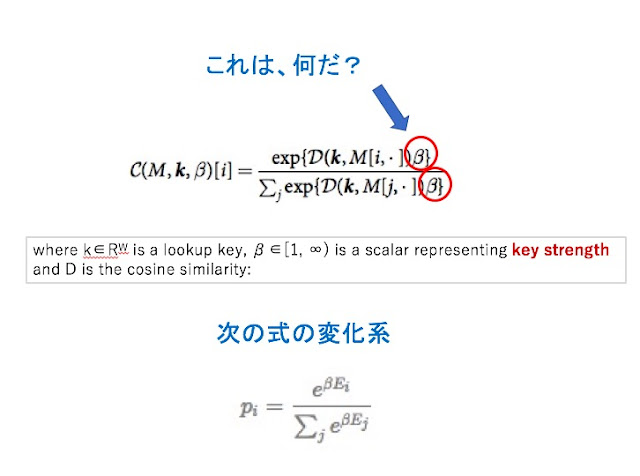
ディープ・ラーニングの「学習」では、様々な「メタ・パラメーター」が登場する。このパラメーターの設定で、学習の精度やスピードが、大きく変わることがある。 こうしたメタ・パラメーターの一つに「温度」が登場することがある。大抵は、Softmaxに確率分布を放り込む時に、一律に一定の定数をかける処理をすることがあるのだが、その定数を「温度」ということがあるのだ。 最初は、この言葉づかいが、奇妙に思えたのだが、昨日見たように、Softmax自体が、物理の理論を借用しているのだと思うと、こうした言葉遣いには、何の不思議もない。頭隠して尻隠さずだ。 最近見かけた例では、GoogleのDeep MindチームのDNC (Differentiable Neural Computer)に、次のような関数が定義されていた。（図１） この関数 C(M, k, β) [i] は、DNCで、もっとも基本的な関数の一つである。ご覧のように、分子でも分母でも、冪乗部分に一律に定数βがかかっている。Nature誌の解説では、このβは、「キーの強さ」だとされている。 でも、この式は、Softmaxの原型である図１の下の式、すなわち、ある分配関数が定義された時、系がある状態i を取る確率を表す式の変化系だと思うのがいいような気がする。 図２に、 β = 1/kBTと、明示的に温度Tが見える形にした時、Tの値をあげたり下げたりした時、この分布がどう変化するかを示してみた。（Ei の分布は変わらないとして） ディープ・ラーニングの学習でのメタ・パラメーター「温度」の役割についても、この関係は基本的に成り立つはずだ。 要するに、「温度」が高いと、いろんなところに複数の比較的高い確率が見られるようになり、「温度」が低いと、一つのピークがはっきりと現れる。（山の凸凹のパターンは、基本的に同じなのだが、コントラストが強調される） 特徴抽出には、後者の方が良さそうに見えるかもしれないが、意外と単純ではない。前者のほうが、収束には時間がかかりそうだが、思いもかけない特徴を発見する可能性があるかもしれないし、後者の方は、実は、つまらない特徴しか見つけられないということになるのかもしれない。 面白いのは、我々の日常の議論にも、こうした類型的には二つのパターンがあるのではないか

Softmaxの対応物を考える さきに、ディープ・ラーニングでよく使われる「クロス・エントロピー」が、もともとのシャノンのエントロピーをベイジアン風に拡大した（という「解釈」が存在するという意味なのだが）「相対エントロピー」の一種だという話をした。 「相対エントロピー」は、「まだ残されている、学習すべき情報」と解釈できるので、ディープ・ラーニングで「クロス・エントロピー」を最小にしようという目標は、この解釈だとわかりやすいと思うという話だった。 今日は、同じくディープ・ラーニングで多用される「Softmax」の話をしようと思う。 クロス・エントロピーと同様に、AIのエンジニアは、天下りでこの関数を使うことが多い。というか、ディープ・ラーニングのフレームワークに、そのまま準備されているので、「使い方」さえ覚えれば、クラスの分類は自動的に実行されるわけで、その「意味」や「成り立ち」を考える必要はないのだが。 ただ、それは、もったいないとも思う。（余計なお世話かな？） 物理から見てSoftmax（に対応する式）が、どういうものかを見てみよう。 ある系の持つ可能な状態の数を考える それには少し準備がいる。 まず、同じ大きさのN個のBoxからなる系を考えよう。それぞれのBoxはk個の状態を持つとしよう。 あるBoxがある状態iを取るとき、次のように線で結ぶ。 この例は、Box1が状態１を取り、Box4が状態2を取り、Box Nが状態4を取ることを表している。Box2, Box3は、この図では線で状態と結ばれていないが、それは、表記上省略しているだけである。 次の図では、Box1が状態2を取り、Box3が状態1を取り、Box4が状態4を取り、Box Nが状態kを取ることを表している。Box2の状態は、この図では省略されている。 全てのBoxは、必ず、何らかの状態を持つのだが（例では省略されていても）、全ての状態が、あるBoxの状態になるとは限らない。次の例では、Box2, Box3, Box4 は、同じ状態2を持っている。 状態iが、何個のBoxで共有されているかを $n_i$で表すことにしよう。先の例では、$n_2=3$ということになる。$ n_1+n_2+n_3+ \cdots + n_k = N

最近、自分の関心が、二つの方向に分裂していることを感じている。 一つは、昨日ミスルトで行なった、「人工知能と私たちの未来 -- 子育てママ教育編」のように、いままであまり接点のなかった人たちとコンタクトしてみたいという関心である。 もう一つは、理論的に、もっと深いところで、我々の科学的な認識がどのように発展しているのかを知りたいという関心である。 前者について言えば、いままで接点のない人とのコンタクトを広げるのは、なかなか難しい。昨日のイベントも集客には苦労して、知っている人に、随分助けてもらった。 でも、楽しかった。少人数でも。 これからも、続けられたらと思う。 ここでは、少し、後者の問題について考えてみたい。 端的に言えば、いままで僕と接点のあった人たち（主要には、ITエンジニアのアーリー・アダプター志向の人たちだと思う）と、こうした僕の関心を、どうしたら共有できるのかという問題である。 問題意識の共有は、できるのではないかと考えている。（僕は、原理的には、楽観論者だ。） なぜなら、情報理論やエントロピーの理解は、人工知能技術を深く理解する上でも、欠かせないのだから。 ただ、話が、少し難しくなる。 例えば、一年前の僕の投稿 あたりは  http://maruyama097.blogspot.com/2017/06/50-lawvere.html 、どうだろう？　もちろん、もっと噛み砕ける。LawvereやRosetta Stoneはおいといても、「相対エントロピー」、「エントロピーのベイジアン的解釈」は、わかりやすく説明できると思う。 人工知能技術だけではない。現代の物理学は、情報理論との接近を強めている。 ブラックホールから情報が取り出せないことを『計算の複雑性』で説明したり、時空を構成する 「tensor network」(紛らわしいが、TensorFlow Network とは、何の関係もない) が「量子エラー訂正回路」だといったりする。面白い。 きっと、次世代のイノベーションの中核となるであろう量子コンピュータの基礎理論は、着々と準備されているのだと思う。IT技術者が、無関心でいい訳はない。 いつか、マルレクで、「IT技術者のための情報理論入門」みたいのが、できればいいと思っている。（だ

一年前のFacebookへの投稿を再掲します。 ---------------------------------------- 今年の冬休みの最大の収穫は、Lawvereのこの論文を見つけたこと。 ”The category of probabilistic mappings -- With Applications to Stochastic Processes, Statistics, and Pattern Recognition" http://goo.gl/53nxEv もともとは、機械学習の損失関数（コスト関数）によく使われる「相対エントロピー」のわかりやすい説明が、John Baezの数年前の論文にあったよなと思って探していたのだが、そこでついでに目に入ったのが、2013年に出ていたFongの次の論文。 Brendan Fong: "Causal Theories: A Categorical Perspective on Bayesian Networks" http://arxiv.org/pdf/1301.6201v1.pdf この論文自体は、ベイジアンの立場からの「因果性の理論」なのだが、その理論的なビジョンは、冒頭で紹介したLawvereの論文に基づいている。 Lawvereの論文1.3節の "Stochastic Processes and Decision Maps「確率過程と決定写像」" を読んでもらいたいのだが、現在の「機械学習」技術の、ほぼ、完璧な特徴づけがある！ Ωをある空間とする。Δを、Ωを「パターン」ごとに分割した空間とする。 「パターン認識」とは、ΩからΔの写像 f を見つけること。 ただし、一般には、Ωは巨大で、全体をスキャンするのも、 f を見つけるのも困難である。 そこで、実際に「観測された状態」からなる Γ を考える。 さらに、ΩからΓへの、次のような確率写像 F を考える。 Ωの基本的な状態の一つをωとする時、Γの部分集合Aに対して、 F(ω, A)は、Aについての条件付きの確率を与える。 δを、ΓからΔの写像とする。 この時、「パターン認識」の問題は、完備化されれば、f = F ・ δ　となるような、最良の写像 δ を求め

ある確率分布 $p_i$が与えられた時、その情報量は、$ - \sum  p_i log(p_i)$ で与えられる（シャノンの情報量）。 （今回は、特に、説明しなかったのだが、「情報量」と「エントロピー」は、同じ概念である。) ただ、どんな確率分布についても、アプリオリに一つの情報量が先の公式で天下り的に定まるということに、すこし違和感を持つ人がいるかもしれない。（僕は、そうだったのだが） そういう人には、次の「相対的な情報量」という考え方の方が、納得が行きやすいと思う。得られる情報量は、絶対的な確定したものではなく、事前に知っていたこととの関係で決まる、相対的なものだと考えるのだ。 事前に知っていた（多分、それは正確な知識ではないかもしれないので「仮説」といってもいい）確率分布を$p_i$ としよう。実際に、観測して新しい確率分布 $q_i$ が得られた時の、 $p$に対する$q$の「相対的情報量」を、次の式で定義する。 $$ I(q,p) = \sum  q_i log (q_i / p_i)$$ $I(q,p)>=0$ で、 $I(q,p)=0$となるのは、$q=p$ の場合だけであることはすぐわかる。 明らかに、先のアプローチは、ベイジアンのものである。「相対的な情報量」というのは、アプリオリな「シャノンの情報量」を、ベイジアンの考え方で、相対化した情報量なのである。 情報量のこの相対的な解釈は、人間の認識で得られる情報量の解釈には、とても向いている。認識や学習のモデルを、この情報量を使って解釈できる。 例えば、先の$I(q,p)=0$の場合の解釈では、仮説$p$と実験結果$q$が一致した場合には、実験で得られた情報量は0 だと考えればいい。 認識の順番を$t$ で表してみよう。先の例では、事前の仮説$p(t-1)$が、実験によって、事後に $q(t)$ に置き換わるのだが、この実験で得られた情報は、$I(q(t), p(t-1))$ で表される。 ここで、$q(t)$を新たな$p(t)$ として、$I(q(t+1), p(t))$ を考える操作を繰り返すことができる。 これは、「認識の発展」のモデルと考えることができる。この「認識の発展」は、$I(q,p)=0$になるときに終わる。 逆に、もしも、最初から正

7月2日、大阪で「ディープラーニング6時間集中講義」の第二弾を開催します。テーマは「自然言語」です。 私たちが普通に使っている「言語」の「意味」を機械に理解させることは、人工知能のもっとも大きな目標の一つです。 多くの関心を集め、応用分野の拡大が続く「人工知能技術」ですが、自然言語処理の分野では、残念ながら、まだまだ多くの課題が残されています。 講演の前半では、ディープラーニング技術に限らずに、自然言語をめぐる様々なトピックを紹介します。アプローチの多様性は、このチャレンジの難しさを示しているのかもしれません。 講演の後半では、ニューラル・ネットワークの側からの取り組みを紹介します。まず、基本的なツールとしての RNN という技術の紹介をし、最後に、この分野での最高の達成の一つである、Googleの「ニューラル機械翻訳」を詳しく見てみたいと思っています。 自然言語処理の現状を理解することは、現在の人工知能技術の到達点を正確に把握する上で不可欠の課題だと考えています。また、それは、人工知能技術の未来を考える上でも、大きな意味を持っています。 多くの皆様の参加をお待ちしています。 開催概要・お申込みについては、次のサイトをご利用ください。 http://osaka-deeplearning2.peatix.com/

次回マルレクを、7月31日 19時から、富士通さんで開催します。 テーマは、「人工知能の歴史を振り返る」です。（先日のABCで行った20分の講演の2時間バージョンです。） 講演概要： 2012年に始まった「ディープラーニング」のブームから、5年がたちました。 ますます応用分野を拡大する人工知能技術が、私たちの生活と未来にとって大きな意味を持つことは、多くの人の共通認識になりつつあります。 同時に、この間の様々な取り組みを通じて、現在の人工知能技術が、克服すべき課題を抱えていることも、明らかになりつつあります。 人工知能の未来を考える上では、現在の到達点を正確に把握することが必要です。また、できるだけ広いパースペクティブの中で、問題を捉えることが重要だと考えています。 講演では、これまでのマルレクで取り上げてきたトピックと比べると、すこし回り道になりますが、あらためて、チューリングから現在までの、人工知能研究の歴史を振り返ってみようと思います。 （写真は、チューリング）