図形の持つ意味

【 図形の持つ意味 】

一つの要素しか持たない集合 1 から集合 X への関数 xで Xの要素 xが表現できるように、オブジェクト 1 からオブジェクト X への stochastic map p で X上の確率分布を表現できます。図形では、1 から Xへ 波線矢印を引くだけで、X の確率分布が表現できます。

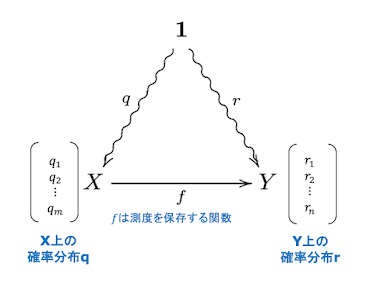
1 と X と Y を頂点とする三角形を考えます。頂点に 1 を、左に X 、右に Yを置きます。1 から Xと Yに波線矢印を引き、XからYに矢印を引きます。

今回のセッションは、この図形がどういう意味を持っているのかという話です。　

1 から Xへ 波線矢印は Xの確率分布、1 から Yへ 波線矢印は Yの確率分布ですので、底辺のXからYへの矢印は 確率分布から確率分布への写像になります。

実は、この三角形が「可換」である時、このXからYへの写像は、XからYへの「測度を保存する関数」であることを示すことができます。ですので、どこかでこれと同じ三角形を見かけたら、その三角形の底辺の性質を、すぐに知ることができます。　


カテゴリー論が強力なのは、図形を見るだけで、その背後にある数学的関係を、別の推論に利用できるようになるからです。

カテゴリー論の図形は具体的で、それを用いた推論も直観的なのですが、その図形の意味するところは、実は、抽象的なものです。

今回、底辺のXからYへの矢印を、具体的に計算可能な形に書いてみました。やらずもがなと思いましたが、図形の抽象的な意味を、具体的な例で納得することは、必要なことだと感じています。　

YouTube :
https://youtu.be/ejSmTPNfBGA?list=PLQIrJ0f9gMcPcLv9Xw1F4OnNfO1d9lxxh

スライドのpdf版は、こちらからアクセスできます。https://drive.google.com/file/d/1cJ5f3hV5tzGh9AEEPSYxtUHyMAFWm6Ak/view?usp=sharing

このシリーズのまとめページは、「エントロピー論の現在・補遺」です。https://www.marulabo.net/docs/info-entropy5-addendum/


コメント

コメントを投稿

このブログの人気の投稿

マルレク・ネット「エントロピーと情報理論」公開しました。

イメージ
前回の秋葉原でのマルレクのネット配信が始まりました。 https://crash.academy/class/156 タイトルを「エントロピーと情報理論 -- 量子情報理論入門 -- 」に変更しました。最初の30分は、無料です。 次回のマルレク「量子コンピュータとは何か？」の導入となるコンテンツです。 講演資料は、こちらです。 https://goo.gl/CKayix  あわせて、ご利用ください。 　　　--------------------------------- 　　　マルレク・ネット　ビデオ・コンテンツ　 　　　--------------------------------- 　「エントロピーと情報理論」 　　　　 https://crash.academy/class/156 　「人工知能の歴史を振り返る」 　　　　 https://crash.academy/class/139/ 　「ニューラル・コンピューターとは何か？」 　　　　 https://crash.academy/class/101/ 　「Google ニューラル機械翻訳」 　　　　 https://crash.academy/class/76/ 　「RNNとLSTMの基礎」 　　　　 https://crash.academy/class/66/
続きを読む

初めにことばありき

旧約の「創世記」の「光よあれ」は、ビッグバンを思わせて、物理学者はちょっと萌えるかもしれないのだが、新約の「ヨハネによる福音書」には、言語学者が喜びそうなフレーズがある。 「初めに言があった。言は神と共にあった。言は神であった。」 僕が知っていたのは、「はじめにことばありき」という訳だったのだが。この口語訳での「言」は、英訳だとこうなっている。 "In the beginning was the Word, and the Word was with God, and the Word was God." 「言」= "Word" である。はじめにあったのは、Wordであって、Language ではない。だから、新しい口語訳では、普段、あまり馴染みない「言」という訳語を使ったのかも。「初めに語があった」では、なんかしまらないんだろうな。（僕は、「はじめにことばありき」というフレーズの方が好きだ。） ちなみに、「ヨハネによる福音書」は、英語では、"Gospel of John" という。「ジョンのゴスペル」である。でも、そう日本語に訳してしまうと、ジョン・レノンがバラードではなく、ゴスペルを歌っているようで、まずいんだろうな。 「ことば」・「言」・"Word" と訳されている、元々の言葉を調べてみると面白い。 キリスト教のオーソドックスな原典であるラテン語訳聖書では、この部分は、こうなる。 "In principio erat Verbum, et Verbum erat apud Deum, et Deus erat Verbum" 「イン・プリンキピオー・エラト・ウェルブム」 英訳 Word のラテン語の原語は、Verbum である。この単語、英語に直訳すれば、Verbである。「初めに、動詞があった。」　言語学の「従属性文法 (Dependency Grammar) 」理論の人たち、喜びそう。 もっとも、英語のVerbは、元々は、動詞というより広く言葉全体をさしてたらしい。そのことは、「ノンバーバル・コミュニケーション (Non-Verbal Communication) 」というのが、動詞を使わないコミュニケーション
続きを読む

人間は、善と悪との重ね合わせというモデルの失敗について

人間は善と悪との「重ね合わせ」だという前回の話は、人間の本性の複雑さを語るのには、ありうる喩えなのかもしれないが、量子の「重ね合わせ」の喩えとしては、実は、二つの点で失敗しているのだ。 一つには、複雑な善と悪との重ね合わせから情報を引き出す「簡単・粗野」な方法として、善か悪かの判断のみを下す「善悪測定器」を、便宜的に導入したのだが、これがマズイ。 複雑な量子の状態を「測定」した時に、我々は、その状態を複雑なまま見いだすことは出来ないのだ。量子が、善と悪との状態の重ね合わせだとしたら、測定によって我々が見いだすのは、必ず、善か悪か、どちらかの状態の量子を見いだす。 もしも、量子が、善悪二つの状態の重ね合わせではなく、もっと沢山の状態（例えば、100個の状態）の重ね合わせの場合でも、我々が「測定」で得られるのは、その中の、たった一つの状態である。 だから、量子の世界では、善か悪かの判断のみを下す「善悪測定器」は、決して「便宜的」なものではなく、これ以外の測定はできないという意味で、「原理的」な制約を表現しているのである。そのことが、先の喩えでは、うまく表現されていない。 量子の不思議さを、「重ね合わせ」の状態が不思議だと思っている人も多いのだが、それは違うと思う。 善と悪との重ね合わせの前回の例もそうだし、波だって、フーリエ変換だって、我々の日常に、たくさん「重ね合わせ」の現象は存在する。それは、ちっとも不思議なことではないし、表象するのも簡単である。 不思議なのは、「重ね合わせ」ではなく、量子に対する「測定」の方なのだ。それは、我々が「測定」に対してもつイメージとは、かけ離れている。量子力学の基礎の部分を構成しているのは、この不思議な「測定」の形式化・数式化なのである。（そして、それは、難しいものではない。今度の「紙と鉛筆」の演習に来て。） 二つ目の失敗も、実は、「測定」の扱いに関係している。 先の例では、丸山は、1,000回ほど「善悪測定器」にかけられ、その結果で、70% 悪人で、30% 善人 だと判定されるみたいな話をした。それが違うのである。 我々が「測定」で得られるのは、「重ね合わせ」を構成する複数の状態の中のたった一つの状態であると書いたのだが、それだけではないのだ。「測定」によって、量子の状態は、「測定」された一
続きを読む