過去・現在・未来

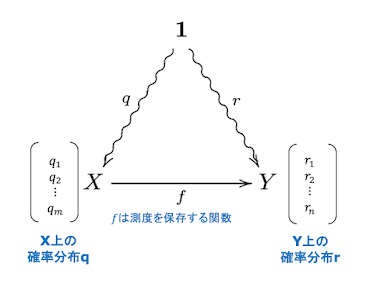
【 chain rule と convex linear 】 先月もエントロピー論のセミナーをしていたのですが、そこでは、エントロピーの特徴づけでは、"Chain Rule" が一番基本的だという話をしました。 今月もエントロピー論のセミナーをしているのですが、そこは、カテゴリー論でエントロピーを特徴づけるというのがトピックスで、"Entropy as a Functor" という見方が、大事だという話をしています。 月が変わるごとに別の話をしているようで、申しわけないんですが、実は二つの話題はつながっています。 今回は、そのつながりを述べてみたいと思います。 エントロピーのFunctorがConvex Linearという性格を持つことは、エントロピーがChain Ruleで特徴づけられることと、とほぼ同じ意味を持っています。  といっても、残念ながら今回の話は、正面からこの二つが同じものだといっているわけではありません。Functor がconvex linear だというためには、chain rule を知ってないとうまくいかないよという話です。 YouTube : https://youtu.be/9q7OScwC2wM?list=PLQIrJ0f9gMcPcLv9Xw1F4OnNfO1d9lxxh スライドのpdfは、次のページからアクセスできます。 https://drive.google.com/file/d/1klb9qJvCYUxyZ7BsS6TvhLZvEAVuISWi/view?usp=sharing このシリーズのまとめページは、「エントロピー論とカテゴリー論」です。 https://www.marulabo.net/docs/info-entropy5-addendum/ セミナーへのお申し込みは、次からお願いします。 https://ent-cat.peatix.com/view お申し込みお待ちしています。

【 6/25ゼミの構成と内容変更しました 】 6/25 マルゼミ「エントロピー論とカテゴリー論」の構成と内容を変更しました。 次のような章立てになっています。 　● 第一部新しいエントロピー論の登場 　● 第二部カテゴリー論的アプローチの基礎 　● 第三部相対エントロピーのカテゴリー論的解釈 　● Appendix Aエントロピー概念の拡大 基本的には、「ツァリス・エントロピー」や「レニ・エントロピー」を紹介した「エントロピー概念の拡大」の章をアペンディックスにまわし、本論では「シャノン・エントロピー」と「相対エントロピー」のカテゴリー論的解釈に集中することにしました。 また、「カテゴリー論的アプローチの基礎」という章を追加して、エントロピー論のカテゴリー論的解釈に関連する概念ツールの基本的な解説を行うことにしました。 あわせて、コンセプトの図解を追加・修正しました。 　○ 「測度を保存する関数」 　○ 「Functor」 　 ○ 「convex linearな関数 」 　○ 「FinStatの二つの射」 このシリーズのまとめページは、「エントロピー論とカテゴリー論」です。 https://www.marulabo.net/docs/info-entropy5-addendum/ セミナーへのお申し込みは、次からお願いします。 https://ent-cat.peatix.com/view お申し込みお待ちしています。

【 図を文章で説明する 】 カテゴリー論で使われる図式は、基本的には、オブジェクト間の関係を射（矢印）で表したものです。 ある図式が可換である（commuteする）というのは、図形上の射を合成したものが、図形上の他の射と等しくなることを言います。図形上の射の合成は、連続して繰り返して行われるかもしれません。 矢印でいえば、図形上の矢印のつながりを追いかけていき、それが図形上の他の矢印に等しくなる時、その図形は可換だと言います。 図形の説明を文章で説明するのは難しいですね。でも、少しやってみましょう。（図で表現すれば一発でわかることを、わざわざ文章で説明しています。） 可換な図式が定義される一番簡単な例は、射の合成が一回だけのもの、合成される二つの射とそれと等しいとされるもう一つの射がある場合、都合三つの射からなる図形の場合です。 A, B, Cを頂点とする三角形があって、AからBに向かう矢印を f, BからCに向かう矢印をg, AからCに向かう矢印を h とします。 この例の場合には、矢印をたどって AからCに行くには、二つ方法があります。一つは、矢印hを使って直接 AからCに向かう方法と、矢印 f, g をたどって  B経由で Cに向かう方法です。二つの方法どちらを選んでも、AからCに到達できます。 これを、矢印 f と矢印 g の「合成」は、矢印 h と「等しい」と言います。こうした時、三角形ABC（矢印を含んで）で表される図形は「可換」だと言います。 図で書けば（あるいは図をイメージすれば）、何を言っているのかすぐにわかるはずです。 何やっているんでしょうね。（図を使わないで、図的な関係を説明しようとしています） 注意してほしいのは、この文章による説明は、可換な三角形の一つの例を、くだくだと説明しているだけで、可換な三角形を全て尽くしているわけではないということです。全部の場合を文章で書くのは、かなり面倒です。 ただ、図をみれば、他の可換な三角形は、どういうものかすぐに理解できます。不思議です。 今回のセッションでは、可換な図式を、いくつか紹介します。もちろん図付きで。 問題は、それからです。可換な図形が何を表現しているか、少し詳しくみてみようと思います。

【「1からの射」】 6/25のセミナーにむけて、基本的な用語と図式の解説を始めています。 カテゴリー論では、図を使うことが多いのですが、それぞれの図はそれぞれの意味を持っています。数式でも同じことを表現できるのですが、だんだん、図の方がわかりやすいと感じるようになります。 今回は「1からの射」という図式 -- 1から矢印が伸びている図式が、どういう意味を持っているのかの説明です。図式というより、図式を構成している図式の断片、図式の「部品」の説明ですね。 部品といえば、この図式の断片に現れる 1 も、ただの数字の1 ではないんです。それは一つの要素しか持たないオブジェクトを表しています。 射 1-> X は、カテゴリー論的には、ざっくりいうとXの要素を表現するのですが、集合Xの要素を「1からXへの射」として捉えるこの解釈は、集合論からカテゴリー論への移行にとって、もっとも基本的なものです。 このセッションでは、この部品を応用して確率分布を表現する方法を述べています。 「1からの射」だけでなく「1への射」も、今回のセミナーでは大事な役割を果たします。今回のセミナーの内容を要約すると「カテゴリー 1へのFunctor」としてエントロピーは解釈できるという話ですので。（Functorも射の一種です） 余談ですが、同じ確率分布に、さまざまな表現があることに注意した方がいいかもしれません。 　確率分布 (X,p) 　確率分布 X 　確率分布 p 文脈にもよりますが、これらは、同じ意味で使われます。紛らわしいかもしれませんね。 YouTube: https://youtu.be/vOy8zK4od7A?list=PLQIrJ0f9gMcPcLv9Xw1F4OnNfO1d9lxxh スライドのpdf版は、こちらからアクセスできます。 https://drive.google.com/file/d/1hdEDX6o3Mm5WiMO90CmTvbur2eJk0qIR/view?usp=sharing このシリーズのまとめページは、「エントロピー論とカテゴリー論」です。 https://www.marulabo.net/docs/info-entropy5-addendum/ セミナーへのお申し込みは、次からお願いします。 https://ent-cat.peatix.com/vi...

【 路線変更 -- もっとわかりやすく！】 連日公開しているセッションは、まだ、「証明」の途中なのですが、セミナーの進め方、変えようと思っています。 先日、セミナーのポイントを知ってもらおうと、基本的なスライドを何枚か公開したのですが、それだけだとかえって分かりにくいことに気づきました。それらは、それぞれ大事なことを示しているのですが、結果だけを並べられてもストーリーがわかりやすくなるとは限りません。 わかりにくいのは、わからないところがあるからです。 議論の細かいところでわからないことがあっても、議論の大まかな流れを理解することはできます。ただ、基本的な術語の意味がわからないままでは、そうした理解も難しくなります。 エントロピー論とカテゴリー論の議論にかかわる基本的な概念を、あらためてきちんと説明してみたいと思います。まわり道ですが、セミナーの内容をわかりやすくするには、それが一番だと思います。 今回は、stochastic mapとmeasure preserving functionを取り上げています。 まだ、すこし、こうした説明を続けたいと思います。そういえば、カテゴリーやFunctorの説明もちゃんとはなかったですね。 今回、measure preserving functionの説明に、「水滴」のたとえを使っています。これは、Parzygnatの論文 "A functorial characterization of von Neumann entropy" から借用したものです。この論文は、量子論的エントロピーのカテゴリー論的解釈を扱ったものです。テーマは、難しいものなのに、説明はわかりやすく丁寧です。いいですね。 YouTube: https://youtu.be/KwojE9tA5Mk?list=PLQIrJ0f9gMcPcLv9Xw1F4OnNfO1d9lxxh スライドのpdf版は、こちらからアクセスできます。 https://drive.google.com/file/d/1gdFAUW_QUiVKE9ojg-4o9MhgRu8GYOM1/view?usp=sharing このシリーズのまとめページは、「エントロピー論とカテゴリー論」です。 https://www.marulabo.net/docs/info-entrop...

【 AとBは同値でも ... 】 AからBが導かれ、かつ、BからAが導かれる時、AとBは同値だと言います。 AとBが同値であることは知っていても（それは、誰かが「AとBは同値である」と言っているのを、たまたま聞いただけかもしれません）、自分で確かめようとするとうまくいかないことがあります。 AとBが同値だということは、AからBを証明でき、BからAを証明できるということなのですが、この二つの証明のわかりやすさが、同じレベルだとは限りません。AからBの証明は易しいのに、逆の、BからAの証明は難しいこともあります。 何を言いたいかと言えば、実は、証明を省略したことの弁解です。 きちんと紹介したかったことは、本当は、次のことです。 「カテゴリーFinStatからカテゴリー [𝟎,∞ ]へのFunctor 𝑅𝐸 が、ある性質を満たすとき、このFunctorが、相対エントロピー を決定することを示すことが出来る。」 ただ、今回のスライドでは、FinStat上の REと相対エントロピー 𝑆(𝑞,𝑝)を対応づけ、相対エントロピー𝑆(𝑞,𝑝)がこの条件を満たすFinStatのFunctor REとみなせることだけを示しています。 これは、必要な証明の半分です。 逆の、この条件を満たすFinStatのFunctorが相対エントロピー 𝑆(𝑞,𝑝)に一致することを示すのは、すこし面倒です。今回はその証明は割愛しています。ごめんなさい。 YouTube : https://youtu.be/83Mr6Xz22vg?list=PLQIrJ0f9gMcPcLv9Xw1F4OnNfO1d9lxxh スライドのpdf版は、こちらからアクセスできます。 https://drive.google.com/file/d/1doZxbHJREHy61lGlaAOfJl_f9sxqRUAW/view?usp=sharing このシリーズのまとめページは、「エントロピー論とカテゴリー論」です。 https://www.marulabo.net/docs/info-entropy5-addendum/

【 観察プロセスをカテゴリー論で表現する 】　 「相対エントロピー」は、これまでも人間の認識や学習のスタイルと結びつけて解釈されてきました。代表的なものは、「相対エントロピーのBayesian的解釈」と言われるものです。また、それらは、Deep Learnig の技術にも大きな影響を与えてきました。 「相対エントロピーのBayesian的解釈」については、マルレクでも、何度か取り上げたことがあります。時間がありましたら、次のムービーをご覧ください。短いものです。 YouTube: 「ディープ・ラーニングとエントロピー  -- 相対エントロピーとその解釈」https://youtu.be/3214xyWSLzo?list=PLQIrJ0f9gMcM2_4wbtngkEvZEYfuv5HY2 このビデオのスライドのpdf: https://drive.google.com/file/d/1e1vyB8rSwegNRXG6CmbrZE-31DlSUAMv/view?usp=sharing 今回のセッションの内容は、それらとはかなり違ったものにみえるかもしれません。ただ、人間の認識の過程を、数学的に表現しようという問題意識は共通のものです。ここで対象となっているのは、あるものを観察するという人間の認識過程です。 あるシステムの状態を、観測機器を使って観測することをイメージしてください。 観測とは、観測の対象であるシステムXの状態を「入力」とし、観測機器の与える観測結果Yを「出力」とするプロセスだと考えることができます。観測のプロセスというのは、システムXの状態を観測機器の状態Yに変換することです。 ただ、あるシステムの状態が、一つの数字で表されるとは限りません。それはいくつかの確率変数の確率分布x∈Xで与えられると考えることができます。同様に、観測結果を示す観測機器の状態yも、確率分布y∈Yで与えられると考えることができます。 観察プロセスを f とした時、この過程を f(x) = y と表します。この見方によれば、観察とは、確率分布として与えられたあるシステムの状態を、やはり確率分布として与えられる観測機器の状態に変換する過程に他ならないということになります。 YouTube : https://youtu.be/MzMQj0xWSzg?list=PLQIrJ0f...

【 図形の持つ意味 】 一つの要素しか持たない集合 1 から集合 X への関数 xで Xの要素 xが表現できるように、オブジェクト 1 からオブジェクト X への stochastic map p で X上の確率分布を表現できます。図形では、1 から Xへ 波線矢印を引くだけで、X の確率分布が表現できます。 1 と X と Y を頂点とする三角形を考えます。頂点に 1 を、左に X 、右に Yを置きます。1 から Xと Yに波線矢印を引き、XからYに矢印を引きます。 今回のセッションは、この図形がどういう意味を持っているのかという話です。　 1 から Xへ 波線矢印は Xの確率分布、1 から Yへ 波線矢印は Yの確率分布ですので、底辺のXからYへの矢印は 確率分布から確率分布への写像になります。 実は、この三角形が「可換」である時、このXからYへの写像は、XからYへの「測度を保存する関数」であることを示すことができます。ですので、どこかでこれと同じ三角形を見かけたら、その三角形の底辺の性質を、すぐに知ることができます。　 カテゴリー論が強力なのは、図形を見るだけで、その背後にある数学的関係を、別の推論に利用できるようになるからです。 カテゴリー論の図形は具体的で、それを用いた推論も直観的なのですが、その図形の意味するところは、実は、抽象的なものです。 今回、底辺のXからYへの矢印を、具体的に計算可能な形に書いてみました。やらずもがなと思いましたが、図形の抽象的な意味を、具体的な例で納得することは、必要なことだと感じています。　 YouTube : https://youtu.be/ejSmTPNfBGA?list=PLQIrJ0f9gMcPcLv9Xw1F4OnNfO1d9lxxh スライドのpdf版は、こちらからアクセスできます。 https://drive.google.com/file/d/1cJ5f3hV5tzGh9AEEPSYxtUHyMAFWm6Ak/view?usp=sharing このシリーズのまとめページは、「エントロピー論の現在・補遺」です。 https://www.marulabo.net/docs/info-entropy5-addendum/

【 具体例でまわり道 】 相対エントロピーのカテゴリー論的再構成で、活躍するのはFinStatというカテゴリーなのですが、このカテゴリーには、stochastiic  mapという、奇妙な写像が登場します。  XからYへの関数は、Xの一つの要素にYの一つの要素を対応づけるのですが、stochastiic  map は、Xの一つの要素にY上の確率分布を対応づけます。Yの確率分布は、Yの一つの要素で表されるものではなく、Yの全ての要素にその要素の確率を割り当てたものの全体です。 こうした、普通の意味では「XからYへの関数」でないものも、カテゴリー論では、「XからYへの射 morphism」として捉えます。 今回は、この関数ではない（その意味ではカテゴリー論らしい）、stochastiic  mapを具体例を挙げてすこし丁寧に説明してみました。わかってしまえば簡単なことなのですが、是非、ゆっくり考えて貰えばと思います。 カテゴリー論らしいと言えば、今回、" x : 1 -> X " という形の射が登場します。 ここで 1 というのは、一つのオブジェクトしか持たないカテゴリーです。 一つの要素しか持たない集合 1 から、集合Xの関数を考えてみましょう。 Xがn個の要素を持つなら、1 から Xへの関数は、1の一つの要素をXのn個の要素に対応づける、n種類だけあることがわかります。これ以外の関数は存在しません。このn個の関数は、Xのn個の要素に、一対一に対応しています。 「xが集合Xの要素である」ことは、「xは 1 -> X の射である」と表現できるのです。 このことは、集合論をカテゴリー論で書き換えた Lawvere の「トポス理論」のもっとも基本的な出発点になりました。 " x : 1 -> X " という形の射は、次回のセッションでも活躍することになります。 YouTube : https://youtu.be/DfzIJtBtSMw?list=PLQIrJ0f9gMcPcLv9Xw1F4OnNfO1d9lxxh スライドのpdf版は、こちらからアクセスできます。 https://drive.google.com/file/d/1c2l_RC8UwwBOYCWdSenf27i1ax8CCNxg/view?u...

【 相対エントロピーをカテゴリー論で捉えかえす 】 新しいセッションを始めようと思います。 この連続セッションでは、相対エントロピーへのカテゴリー論的アプローチとして、BaezとFritzの2014年の論文 ”A Bayesian Characterization of Relative Entropy” を紹介します。https://arxiv.org/abs/1402.3067v2　 この論文は、先に紹介した、エントロピー論に、”Entropy As a Functor” という視点を初めて導入した、Baez, Fritz, Leinster の 2011年の論文 “A Characterization of Entropy in Terms of Information Loss” の続編です。https://arxiv.org/abs/1106.1791v3 今回は、この論文の概要を示して、エントロピーをカテゴリー論で捉え返すとはどういうことなのか説明しようと思います。 つづいて、そもそも相対エントロピーとはどういうものかを、その Baysian 的解釈を中心にお話ししようと思います。この部分は、以前のセミナー「情報とエントロピー」https://www.marulabo.net/docs/info-entropy2/ のふりかえりになっています。 YouTube: https://youtu.be/RVm3oer2cm8?list=PLQIrJ0f9gMcPcLv9Xw1F4OnNfO1d9lxxh スライドのpdf版は、こちらからアクセスできます。 https://drive.google.com/file/d/1bV5YdteRvraptSR3L4ggG7W0SyPgWXwQ/view?usp=sharing このシリーズのまとめページは、「エントロピー論の現在・補遺」です。 https://www.marulabo.net/docs/info-entropy5-addendum/

【 地道に計算する 】 今回も、地道な計算が続きます。（風邪も抜けないし） Rényiエントロピーを定義して、それと前回見たTsallisエントロピーとの関係を見ていきます。基本的には、RényiエントロピーはTsallisエントロピーで表すことができるし、逆に、TsallisエントロピーはRényiエントロピーで表すことができます。それを計算で示していきます。計算自体は、一直線ですが、式が汚いですね。あまり楽しくないと思います。 ただ、RényiエントロピーからHill number という量を導入すると、すこし式が整理されて、見通しが良くなります。 実は、このHill数は「生物多様性」の議論で、重要な役割を果たすのですが、もう少し元気になったら、このあたりの話をしたいと思っています。 YouTube : https://youtu.be/SRA8sxyIxyg?list=PLQIrJ0f9gMcPcLv9Xw1F4OnNfO1d9lxxh スライドのpdf版は、こちらからアクセスできます。 https://drive.google.com/file/d/1alt-W7jzdps8mL8ldhBVEPjzqWMEWa8a/view?usp=sharing このシリーズのまとめページは、「エントロピー論の現在・補遺」です。https://www.marulabo.net/docs/info-entropy5-addendum/

【 Tsallis エントロピーの式を導く 】 寒い日が続いて、風邪をひいてしまいました。 そういうわけで、今回は、カテゴリ〜論抜きでやさしい話です。Tsallis エントロピーの式を導いてみます。 風邪のせいか、証明間違えていました。修正版に差し替えました。 YouTube : https://youtu.be/izTpR22yqg0?list=PLQIrJ0f9gMcPcLv9Xw1F4OnNfO1d9lxxh 修正版のスライドのpdf版は、こちらからアクセスできます。 https://drive.google.com/file/d/1aihp-ARxkMz4WhvbVuQHaiktahQui7gM/view?usp=sharing このシリーズのまとめページは、「エントロピー論の現在・補遺」です。 https://www.marulabo.net/docs/info-entropy5-addendum/

【 カテゴリーとして実数を捉える 】  ShannonエントロピーとTsallisエントロピーがFunctorであるという議論をしてきたのですが、そこでの重要な論点は、エントロピーが取る非負の実数[0, ∞)という値の範囲そのものが、カテゴリーとみなすことができるということです。 ただ、実数をカテゴリーとして捉えることができるということは、自明ではありません。 実数 [0,∞)をカテゴリーと見るアイデアは、1973年のF.  W. Lawvereの論文 “Metric spaces, generalized logic and closed categories” によるものです。 確率分布のカテゴリーから [0, ∞)というカテゴリーへの、ある性質を満たすFunctor 𝐹は、シャノン・エントロピーを一意に決定するという発見が重要なのですが、その議論はすこし複雑です。 ここでは、それよりはやさしい、その逆の、シャノン・エントロピーの差で表現される「情報の損失」は、Functor とみなせることを例に、「実数というカテゴリー」の理解にフォーカスしてみようと思います。 YouTube: https://www.youtube.com/watch?v=loeYIBKTBwM&list=PLQIrJ0f9gMcPcLv9Xw1F4OnNfO1d9lxxh&index=2 スライドのpdf版は、こちらからアクセスできます。https://drive.google.com/file/d/1aD8wyEDgQGfKl-hz8dMflO4GIMxZUO-R/view?usp=sharing このシリーズのまとめページは、こちらです。 https://www.marulabo.net/docs/info-entropy5-addendum/