Google機械翻訳に注目!
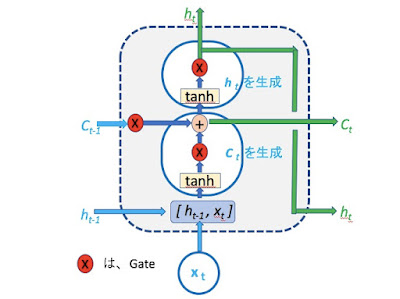
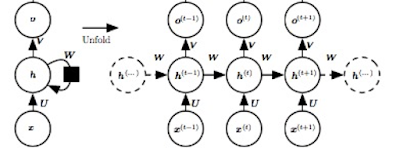
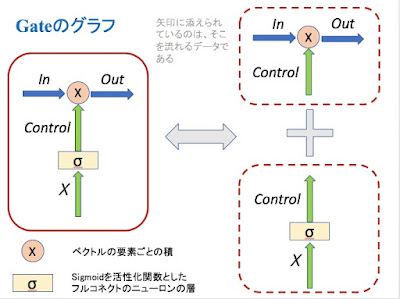
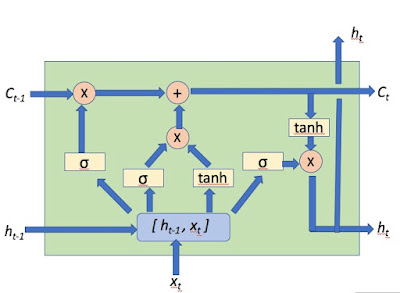
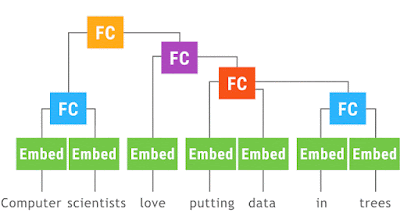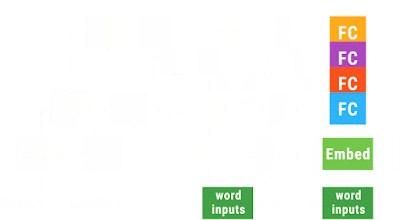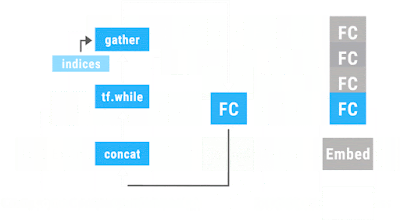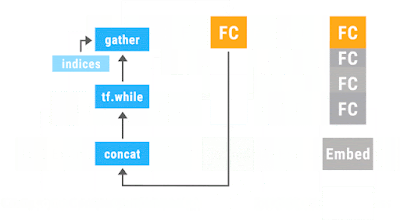
科学でも技術でも、その発展には、飛躍がある。もちろん、飛躍にも小さいものから大きいものまでいろいろあるのだが。 面白いことに、何かが共鳴するように、いろんな飛躍が、ある時期に集中して起きることがある。 人工知能の分野では、2012年がそうした時期であった。ImageNetの画像認識の国際的コンテストで、CNNを使ったAlexNetが圧勝し、Googleの巨大なシステム DistBeliefが、教師なしでも猫の認識に成功する。それが、2012年だ。 この時から、人工知能ブームが起き、技術的には、ニューラル・ネットワークを用いたDeep Learning技術が花形となる。そして、そうした技術的な達成は、ただちに、ビジネスの世界で応用を見つけ出していく。 現在、各社が取り組んでいる自動運転技術と、Alexa, Google Now, Siri 等のボイス・アシスタント・システムが、コンシューマー向けのAIプロダクトとしては、最も大きなマーケットになるのだが、そこでは、Deep Learning技術のCNNが、中心的な役割を演じている。 ただ、技術の変化は早い。 今また、2012年のブレークスルーに匹敵する目覚ましい飛躍が、AIの世界で起きようとしている。昨年11月にサービスが始まった、Googleの「ニューラル機械翻訳」がそのさきがけである。 そこで使われている技術は、RNN/LSTMと呼ばれるものである。 Googleの新しい機械翻訳のシステムは、LSTMのお化けのような巨大なシステムなのだが、その基本原理を理解することは、誰にでもできる。(今度のマルレクにいらしてください) 2012年に続く、この第二の飛躍が、どのようにビジネスに生かされるかは、まだ未知数だが、必ず、現実の世界で利用されていくようになるだろう。 今の眼で、2012年の「Googleの猫」のDistBeliefを振り返れば、かつては驚嘆して見上げたそのシステムが、ハードワイアーでプログラミングをしていた、かつての「巨大システム」ENIACのようなものに、見える。 Googleの機械翻訳のシステムも、いずれ、スマートフォンに収まるようになるだろう。僕の好きな「翻訳こんにゃく」は、早晩、実現されるだろう。 さらに、変化は加速している。 第三の飛