任意のf(x)を計算する量子回路を考える
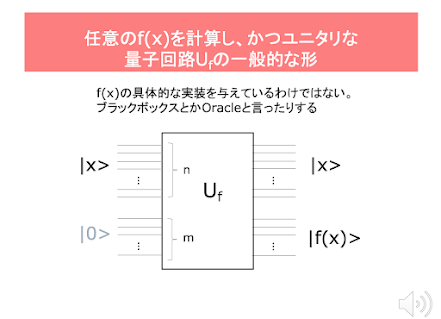
【 任意のf(x)を計算する量子回路を考える 】 Mahadev の論文を読む上で必要な準備をしています。 前回は、ポスト量子暗号のLWE (Learning with Errors)が、古典コンピュータで実装できるアルゴリズムだということを紹介しました。Mahadevの方法は、この古典的に実装可能なLWE暗号を量子コンピュータは破ることはできないということを前提にしています。 Mahadevは、古典コンピュータと量子コンピュータを「対話」させます。正確にいうと、古典コンピュータと人間が一緒にチームを作って、その混合チームを量子コンピュータと対話させます。この対話は「対戦」でもあります。対戦しているのは古典コンピュータと人間の混合チームと単独の量子コンピュータです。 なぜ、人間と古典コンピュータが、同じ仲間になるのかと言えば、量子コンピュータとの関係では、両者は共に同じような能力しか持っていないからなのですが、そこは、「いや、コンピュータ(古典)より、人間がエライ」「そんなことはない。AIをみろ。人間はコンピュータ(でも古典)にかなわない」という議論はあるでしょうが、それは等しく古典的なものの内輪揉めとして、先に進みます。納得いかない人も多いと思いますので、それについては、次回に説明します。 対話あるいは対戦は、古典チームが量子コンピュータにある計算の実行を指示することで始まります。量子コンピュータはそれを計算しその結果を古典チームに返します。古典チームは、その結果を見て新しい指示を量子コンピュータに出します。こうしたことを繰り返します。 量子コンピュータは、古典族と同様に計算を行う能力を持つのですが、その計算のスタイルは、ちょっと変わっています。今回のビデオのセッションは、そのことにフォーカスしています。 関数を計算する量子回路を考えます。量子回路は、量子ゲートから構成されているのですが、量子ゲートは、すべて「ユニタリ性」という性質を持ちます。その結果、量子回路自体も「ユニタリ性」を持つことになります。 量子回路のユニタリ性というのは、簡単に言えば、入力から出力を返す量子回路は、入力と出力を鏡に移したように回路ごと反転させれば、出力から入力を得ることができるという性質です。計算結果の出力から、時間を遡ったように入力を復元できると考えることもできます。これを...